អនុគមន៍ហ្គាំម៉ា

ទំព័រគំរូ:កណ្តាល

ក្នុងគណិតវិទ្យា អនុគមន៍ហ្គាំម៉ា (តាងដោយអក្សរធំក្រិច Γ) ជាបន្លាយនៃអនុគមន៍ហ្វាក់តូរ្យែលចំពោះចំនួនពិត និង ចំនួនកុំផ្លិច។ ចំពោះចំនួនកុំផ្លិច z ដែលផ្នែកពិតជាចំនួនពិតវិជ្ជមាន អនុគមន៍ហ្គាំម៉ាកំនត់ដោយ

$\mathrm{\Gamma }(z)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{t}^{z-1}{e}^{-t}dt$

និយមន័យនេះអាចត្រូវបានគេពន្លាតចំពោះប្លង់កុំផ្លិច លើកលែងតែចំនួនគត់មិនវិជ្ជមាន។

ប្រសិនបើ n ជាចំនួនគត់វិជ្ជមាន នោះគេបាន

$\mathrm{\Gamma }(n)=(n-1)!$

ទំនាក់ទំនងនេះ​បង្ហាញថា​អនុគមន៍ហ្គាំម៉ា​ជាប់ទាក់ទងទៅនឹង​អនុគមន៍ហ្វាក់តូរ្យែល។ អនុគមន៍ហ្គាំម៉ាផ្សារភ្ជាប់ទៅនឹងអនុគមន៍ហ្វាក់តូរ្យែលចំពោះតំលៃ n ជាចំនួនកុំផ្លិច និង មិនមែនជាចំនួនគត់។

អនុគមន៍ហ្គាំម៉ាជាសមាសភាពមួយនៅក្នុងអនុគមន៍របាយប្រូបាបផ្សេងៗ និង ត្រូវបានគេទៅអនុគមន៍ក្នុងវិស័យជាច្រើននៃប្រូបាប ស្ថិតិវិទ្យា ក៏ដូចជាក្នុងវិភាគបន្សំផងដែរ។

និយមន័យ

តំលៃដាច់ខាត​(ម៉ូឌុល)​នៃ​អនុគមន៍ហ្គាំម៉ាក្នុង​ប្លង់កុំផ្លិច

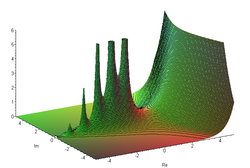
និមិត្តសញ្ញា $\mathrm{\Gamma }(z)$ ត្រូវបានកំនត់ដោយ អាដ្រៀន ម៉ារី ឡេហ្សង់ (Adrien-Marie Legendre ) ។ ប្រសិនបើផ្នែកពិតនៃចំនួនកុំផ្លិច z ជាចំនួនវិជ្ជមាន (Re[z] > 0) នោះអាំងតេក្រាល

$\mathrm{\Gamma }(z)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{t}^{z-1}{e}^{-t}dt$

ទាល់ជាដាច់ខាត (converges absolutely) ។ ដោយប្រើអាំងតេក្រាលដោយផ្នែក គេអាចបង្ហាញថា

$\mathrm{\Gamma }(z+1)=z\mathrm{\Gamma }(z)(1)$

សមីការអនុគមន៍នេះសិក្សាជាទូទៅនូវទំនាក់ទំនង $n!=n(n-1)!$ នៃអនុគមន៍ហ្វាក់តូរ្យែល។ យើងអាចវាយតំលៃដោយការវិភាគ $\mathrm{\Gamma }(1)$:

$\mathrm{\Gamma }(1)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{e}^{-t}dt=\underset{k\to \mathrm{\infty }}{\lim }-e^{-t}{|}_0^k=-0-(-1)=1$

ដាក់ទំនាក់ទំនងទាំងពីរនេះបញ្ចូលគ្នា គេបានករណីពិសេសនៃអនុគមន៍ហ្គាំម៉ា ចំពោះគ្រប់ចំនួនគត់ធម្មជាតិ n ៖

$\mathrm{\Gamma }(n+1)=n\mathrm{\Gamma }(n)=\cdots =n!\mathrm{\Gamma }(1)=n!$

និយមន័យផ្សេងទៀត

និយមន័យផលគុណមិនកំនត់ចំពោះអនុគមន៍ហ្គាំម៉ា រៀងគ្នាតាមអឺលែរ និង វ៉េអែរស្ត្រាស (Weierstrass) គឺត្រឹមត្រូវចំពោះគ្រប់ចំនួនកុំផ្លិច z ដែលមិនមែនជាចំនួនមិនអវិជ្ជមាន:

$\mathrm{\Gamma }(z)=\underset{n\to +\mathrm{\infty }}{\lim }\frac{n!n^z}{z(z+1)\cdots (z+n)}$

$\mathrm{\Gamma }(z)=\frac{e^{-\gamma z}}{z}\prod _{n=1}^{+\mathrm{\infty }}{(1+\frac{z}{n})}^{-1}{e}^{z/n}$

ដែល $\gamma$ ជាថេរអឺលែរ-ម៉ាសឆេរ៉ូនី (Euler-Mascheroni constant)

គេអាចបង្ហាញដោយចំៗថានិយមន័យអឺលែរផ្ទៀងផ្ទាត់សមីការ (1) ខាងលើ ។ អោយ z មិនស្មើនឹង 0, -1, -2, ...

$\begin{array}{cc}\mathrm{\Gamma }(z+1)& =\underset{n\to \mathrm{\infty }}{\lim }\frac{n!n^{z+1}}{(z+1)(z+2)\cdots (z+1+n)}\\ & =\underset{n\to \mathrm{\infty }}{\lim }\left(z\frac{n!n^z}{z(z+1)(z+2)\cdots (z+n)}\frac{n}{(z+1+n)}\right)\\ & =z\mathrm{\Gamma }(z)\underset{n\to \mathrm{\infty }}{\lim }\frac{n}{(z+1+n)}\\ & =z\mathrm{\Gamma }(z)\\ \end{array}$

វិធីផ្សេងទៀតវាអាចត្រូវបានគែបង្ហាញថា...

$\mathrm{\Gamma }(z+1)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{e}^{-t^{1/z}}dt$

ការទាញរកទំនាក់ទំនងជាមួយហ្វាក់តូរ្យែលដោយប្រើអាំងតេក្រាលដោយផ្នែក

វាជាការងាយក្នុងការរក $\mathrm{\Gamma }(1)$

$\mathrm{\Gamma }(1)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{e}^{-x}{x}^{1-1}dx=\underset{0}{\overset{\mathrm{\infty }}{\int }}{e}^{-x}dx=-e^{-\mathrm{\infty }}-(-e^0)=0-(-1)=1$

បន្ទាប់មកយើងទាញរកកន្សោម $\mathrm{\Gamma }(n+1)$ ជាអនុគមន៍នៃ $\mathrm{\Gamma }(n)$:

$\mathrm{\Gamma }(n+1)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{e}^{-x}{x}^{n+1-1}dx=\underset{0}{\overset{\mathrm{\infty }}{\int }}{e}^{-x}{x}^{n}dx$

ដើម្បីដោះស្រាយអាំងតេក្រាលនេះ យើងប្រើអាំងតេក្រាលដោយផ្នែក

$\underset{0}{\overset{\mathrm{\infty }}{\int }}{e}^{-x}{x}^{n}dx={\left[\frac{-x^n}{e^x}\right]}_0^{\mathrm{\infty }}+n\underset{0}{\overset{\mathrm{\infty }}{\int }}{e}^{-x}{x}^{n-1}dx$

យើងឃើញថា $\frac{-0^n}{e^0}=\frac{0}{1}=0$ ។

តាមច្បាប់ឡួពីតាល់ (L'Hôpital's rule) យើងបាន

$\underset{x\to \mathrm{\infty }}{\lim }\frac{-x^n}{e^x}=\underset{x\to \mathrm{\infty }}{\lim }\frac{-n!\cdot x^0}{e^x}=0$

ហេតុនេះតួទី១ ${\left[\frac{-x^n}{e^x}\right]}_0^{\mathrm{\infty }}$ មានលីមីតស្មើនឹង ០ ។ គេបាន

$\mathrm{\Gamma }(n+1)=n\underset{0}{\overset{\mathrm{\infty }}{\int }}{e}^{-x}{x}^{n-1}dx$

អង្គខាងស្តាំនៃសមីការនេះមានតំលៃ $n\mathrm{\Gamma }(n)$ ។ យើងទទួលបានទំនាក់ទំនង

$\mathrm{\Gamma }(n+1)=n\mathrm{\Gamma }(n)$

ដោយប្រើរូបមន្ត យើងទាញបាន

$\mathrm{\Gamma }(2)=\mathrm{\Gamma }(1+1)=1\mathrm{\Gamma }(1)=1!$

$\mathrm{\Gamma }(3)=\mathrm{\Gamma }(2+1)=2\mathrm{\Gamma }(2)=2\cdot 1!=2!=2$

$\mathrm{\Gamma }(4)=\mathrm{\Gamma }(3+1)=3\mathrm{\Gamma }(3)=3\cdot 2!=3!=6$

$\mathrm{\Gamma }(n+1)=n\mathrm{\Gamma }(n)=n\cdot (n-1)!=n!$

តំលៃពិសេស

ខាងក្រោមនេះជាតំលៃពិសេសមួយចំនួននៃអនុគមន៍ហ្គាំម៉ា និង ដេរីវេរបស់វា តំលៃនៃ​ $\mathrm{\Gamma }(1/2)$ អាចអោយគេទាញបានរូបមន្តរកតំលៃពិសេសផ្សេងទៀត។

$\mathrm{\Gamma }(1-z)\mathrm{\Gamma }(z)=\frac{\pi }{\sin \pi z}$

ចំពោះ $z=\frac{1}{2}$ គេទាញបាន:

$\mathrm{\Gamma }(1/2)=\sqrt{\pi }$

តាមរយៈតំលៃនេះគេអាចកំនត់បានតំលៃពិសេសផ្សេងទៀត

$\mathrm{\Gamma }(-3/2)=\frac{4\sqrt{\pi }}{3}$

$\mathrm{\Gamma }(-1/2)=-2\sqrt{\pi }$

$\mathrm{\Gamma }(1/2)=\sqrt{\pi }$

$\mathrm{\Gamma }(1)=0!=1$

$\mathrm{\Gamma }(3/2)=\frac{\sqrt{\pi }}{2}$

$\mathrm{\Gamma }(2)=1!=1$

$\mathrm{\Gamma }(5/2)=\frac{3\sqrt{\pi }}{4}$

$\mathrm{\Gamma }(3)=2!=2$

$\mathrm{\Gamma }(7/2)=\frac{15\sqrt{\pi }}{8}$

$\mathrm{\Gamma }(4)=3!=6$

និងក្នុងករណីទូទៅ:

$\mathrm{\Gamma }(n+\frac{1}{2})=(n-\frac{1}{2})\mathrm{\Gamma }(n-\frac{1}{2})=(n-\frac{1}{2})(n-\frac{3}{2})\cdots \frac{3}{2}\frac{1}{2}\mathrm{\Gamma }\left(\frac{1}{2}\right)=\frac{(2n)!}{2^{2n}n!}\sqrt{\pi }$

ទំនាក់ទំនងរវាងដេរីវេ និង $\gamma$ ថេរអឺលែរ-ម៉ាសឆេរ៉ូនី:

${\mathrm{\Gamma }}^{\prime }(1/2)=-\sqrt{\pi }(\gamma +2\ln (2))$

${\mathrm{\Gamma }}^{\prime }(1)=-\gamma$

${\mathrm{\Gamma }}^{\prime }(2)=1-\gamma$

${\mathrm{\Gamma }}^{″}(1/2)=\sqrt{\pi }(\gamma +2\ln (2){)}^2+\frac{{\pi }^{5/2}}{2}$

${\mathrm{\Gamma }}^{″}(1)={\gamma }^2+\frac{{\pi }^2}{6}$

${\mathrm{\Gamma }}^{″}(2)=(1-\gamma {)}^2+\frac{{\pi }^2}{6}-1$