រូបមន្តដឺម័រ

រូបមន្តដឺម័រ (De Moivre's formula) ត្រូវបានគេហៅដោយយកតាមឈ្មោះរបស់លោក អាប្រាហាម ដឺ ម័រ (Abraham de Moivre) ដែលជាជនជាតិបារាំង ដោយបានចែងថាចំពោះគ្រប់ចំនួនកុំផ្លិច (និងជាពិសេសចំពោះគ្រប់ចំនួនពិត) x និង គ្រប់ចំនួនគត់ n គេបាន

${(\cos x+i\sin x)}^n=\cos \left(nx\right)+i\sin \left(nx\right)$

រូបមន្តនេះមានសារៈសំខាន់ពីព្រោះវាភ្ជាប់ចំនួនកុំផ្លិច (i តំណាងអោយឯកតានិម្មិត) និង ត្រីកោណមាត្រ ។ កន្សោម $\cos x+i\sin x$ គឺជួនការត្រូវបានគេសរសេរកាត់ជា $cisx$ ។

ការទាញយករូបមន្តដឺម័រ

រូមមន្តដឺម័រអាចត្រូវបានទាញចេញដោយងាយដោយប្រើរូបមន្តអយល័រ

$e^{ix}=\cos x+i\sin x$

និងតាមទ្រឹស្តីបទអិចស្ប៉ូណង់ស្យែល

${\left(e^{ix}\right)}^n=e^{inx}$ ។

តាមរូបមន្តអយល័រ គេបាន

$e^{i(nx)}=\cos (nx)+i\sin (nx)$ ។

សំរាយបញ្ជាក់រូបមន្ត

គេមាន $x\in ℝ$

យើងសិក្សា៣ករណី

(១). ករណី $n>0$ យើងបកស្រាយប្រើវិចារកំនើន។ នៅពេល $n=1$ លទ្ធផលគឺពិតជាត្រឹមត្រូវ។ តាមសម្មតិកម្ម យើងសន្មតថាលទ្ធផល​គឺពិតចំពោះ​គ្រប់ចំនួនគត់វិជ្ជមាន $k$ គឺថា

${(\cos x+i\sin x)}^k=\cos \left(kx\right)+i\sin \left(kx\right)$

យើងបាន

• ចំពោះ $n=1;\Rightarrow (\cos x+i\sin x{)}^1=\cos (1\cdot x)+i\sin (1\cdot x)$ទំព័រគំរូ:Spaces ពិត
• ចំពោះ $n=2;$
  $\begin{array}{cc}\Rightarrow (\cos x+i\sin x{)}^2& ={\cos }^{2}x-{\sin }^{2}x+2i\cos x\sin x\\ & =\cos (2\cdot x)+i\sin (2\cdot x)\\ \end{array}$
  សមីការផ្ទៀងផ្ទាត់ចំពោះ n = 2 ដែរ

• ឧបមាថាវាពិតដល់ $n=k+1$ គេបាន

$\begin{array}{cc}{(\cos x+i\sin x)}^{k+1}& ={(\cos x+i\sin x)}^k(\cos x+i\sin x)\\ & =[\cos \left(kx\right)+i\sin \left(kx\right)](\cos x+i\sin x)& & \\ & =\cos \left(kx\right)\cos x-\sin \left(kx\right)\sin x+i[\cos \left(kx\right)\sin x+\sin \left(kx\right)\cos x]\\ & =\cos \left[(k+1)x\right]+i\sin \left[(k+1)x\right]& & \end{array}$

យើងសន្និដ្ឋានថាលទ្ធផលពិតចំពោះ $n=k+1$ នៅពេលដែល $n=k$ ។ តាមគោលការណ៍វិចារកំនើនគណិតវិទ្យា លទ្ធផលពិតចំពោះគ្រប់ចំនួនគត់វិជ្ជមាន $n\ge 1$

(២). ករណី $n=0$ រូបមន្តពិតព្រោះ $\cos (0x)+i\sin (0x)=1+i0=1$, គេអាចសន្មត $z^0=1$ ។

(៣). ករណី $n<0$ យើងសន្មតមានចំនួនពិតវិជ្ជមាន $m$ ដែល $n=-m$ ។ ដូចនេះ

$\begin{array}{cc}{(\cos x+i\sin x)}^n& ={(\cos x+i\sin x)}^{-m}\\ & =\frac{1}{{(\cos x+i\sin x)}^m}\\ & =\frac{1}{(\cos mx+i\sin mx)}\\ & =\cos \left(mx\right)-i\sin \left(mx\right)\\ & =\cos (-mx)+i\sin (-mx)\\ & =\cos \left(nx\right)+i\sin \left(nx\right)\end{array}$

ដូចនេះរូបមន្តពិតចំពោះគ្រប់តំលៃជាចំនួនគត់នៃ n ។

លក្ខណៈទូទៅ

ប្រសិនបើ z និង w' គឺជាចំនួនកុំផ្លិច នោះគេបាន

${(\cos z+i\sin z)}^w$

គឺជាអនុគមន៍មានតំលៃច្រើន ដែល

$\cos (wz)+i\sin (wz)$

មិនមែន។ ដូចនេះគេអាចពោលថា

$\cos (wz)+i\sin (wz)$ទំព័រគំរូ:Spacesគឺជាតំលៃមួយនៃទំព័រគំរូ:Spaces${(\cos z+i\sin z)}^w$

គំនូសមនៅលើ ប្លង់កុំផ្លិចនៃរឹសគូបនៃ១

អនុវត្ត

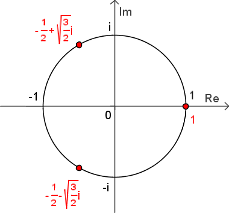
រូបមន្តនេះអាចត្រូវបានគេប្រើប្រាស់ដើម្បីរករឹសទី n នៃចំនួនកុំផ្លិច។ ប្រសិនបើ z ជាចំនួនកុំផ្លិច សរសេរក្នុងទំរង់ប៉ូលែរជា

$z=r(\cos x+i\sin x)$

គេបាន

$z^{{}^{\frac{1}{n}}}={\left[r(\cos x+i\sin x)\right]}^{{}^{\frac{1}{n}}}=r^{{}^{\frac{1}{n}}}[\cos \left(\frac{x+2k\pi }{n}\right)+i\sin \left(\frac{x+2k\pi }{n}\right)]$

ដែល k ជាចំនួនគត់។ ដើម្បីទទួល n រឹសផ្សេងៗគ្នានៃ z ចាំបាច់ត្រូវការអោយតំលៃនៃ k ពី 0 ដល់ n-1 ។

សូមមើលផងដែរ

• រូបមន្តអយល័រ (Euler's formula)
• ចំនួនកុំផ្លិច