ទ្រឹស្ដីបទវ៉ារីញ៉ុង

មានទ្រឹស្ដីបទវ៉រីញ៉ុង(Varignon's theorem)២គឺ មួយនៅក្នុងគណិតវិទ្យា និងមួយទៀតនៅក្នុងមេកានិច។ ទ្រឹស្ដីបទទាំង២នេះត្រូវបានបកស្រាយដោយគណិតវិទូបារាំងឈ្មោះ ព្យែរ វ៉ារីញ៉ុង [Pierre Varignon (1654 – 1722)]។

ទ្រឹស្ដីបទវ៉ារីញ៉ុងនៅក្នុងគណិតវិទ្យា

ទ្រឹស្ដីបទនេះត្រូវបានបកស្រាយនៅឆ្នាំ១៧៣១។ ទ្រឹស្ដីបទនេះនិយាយអំពីរបៀបសង់ប្រលេឡូក្រាម(គេឱ្យឈ្មោះថាប្រលេឡូក្រាមវ៉ារីញ៉ុង)ពីចតុកោណសមញ្ញ។ ពំនោលទ្រឹស្ដី៖

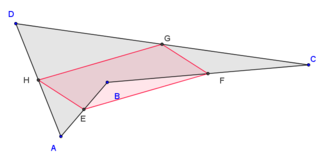
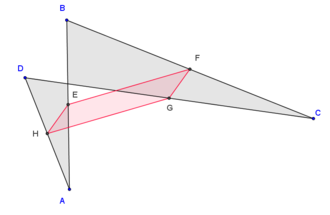
ចំណុចកណ្ដាលនៃជ្រុងរបស់ចតុកោណមួយ បង្កើតបានជាប្រលេឡូក្រាមមួយ។ ក្នុងករណីដែលចតុកោណនោះជាចតុកោណប៉ោងឬផត ក្រឡាផ្ទៃរបស់ប្រលេឡូក្រាមនោះស្មើនឹងពាក់កណ្ដាលក្រឡាផ្ទៃរបស់ចតុកោណទាំងមូល។

ប្រសិនបើយើងគិតពីសញ្ញាណផ្ទៃមានទិសដៅ ទ្រឹស្ដីបទនេះក៏ផ្ទៀងផ្ទាត់ក្នុងករណីចតុកោណខ្វែងដែរ។

ចតុកោណប៉ោង	ចតុកោណផត	ចតុកោណខ្វែង

សម្រាយបញ្ជាក់

ដោយអនុវត្តទ្រឹស្ដីបទចំណុចកណ្ដាល យើងស្រាយបញ្ជាក់ថាជ្រុងឈម២ៗនៃចតុកោណ $I J K L$ ស្របនឹងអង្កត់ទ្រូងរបស់ចតុកោណ $A B C D$ ហេតុនេះចតុកោណ $I J K L$ ជាប្រលេឡូក្រាម។

យើងយកប្រវែង $\overline{B D}$ ស្មើនឹង $d$ កម្ពស់របស់ត្រីកោណ ABD និង CBD គឺ $h_{1}$ និង $h_{2}$ ។ ដោយប្រើទ្រឹស្ដីបទតាលែស គេបាន បាតរបស់ប្រលេឡូក្រាមស្មើនឹង $\frac{1}{2} d$ ហើយកម្ពស់ $h = \frac{1}{2} (h_{1} + h_{2})$ ។

S_{I J K L} = \frac{1}{2} d . \frac{1}{2} (h_{1} + h_{2}) = \frac{1}{2} (\frac{1}{2} d . h_{1} + \frac{1}{2} d . h_{2}) = \frac{1}{2} (S_{A B D} + S_{C B D}) = \frac{1}{2} S_{A B C D}